Sila lihat penerangan tentang Fibonaci number dalam : http://en.wikipedia.org/wiki/Fibonacci_number
Fibonaci number ini telah banyak digunakan untuk penerangan saintifik malahan juga digunakan meramalkan kedudukan saham- saham dalam naik dan turun.
List of Fibonacci numbers
The first 21 Fibonacci numbers (sequence A000045 in OEIS), also denoted as Fn, for n = 0, 1, 2, ... ,20 are:[8][9]
-
F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15 F16 F18 F19 F20 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 2584 4181 6765
Using the recurrence relation, the sequence can also be extended to negative index n. The result satisfies the equation
Thus the complete sequence is
Closed form expression
Like every sequence defined by linear recurrence, the Fibonacci numbers have a closed-form solution. It has become known as Binet's formula, even though it was already known by Abraham de Moivre:
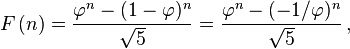 where
where 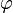 is the golden ratio
is the golden ratio (sequence A001622 in OEIS)
(sequence A001622 in OEIS)
(note, that 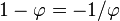 , as can be seen from the defining equation above).
, as can be seen from the defining equation above).
Fibonacci numbers in nature

Fibonacci sequences appear in biological settings,[35] in two consecutive Fibonacci numbers, such as branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple,[36] the flowering of artichoke, an uncurling fern and the arrangement of a pine cone.[37] In addition, numerous poorly substantiated claims of Fibonacci numbers or golden sections in nature are found in popular sources, e.g. relating to the breeding of rabbits, the spirals of shells, and the curve of waves[citation needed]. The Fibonacci numbers are also found in the family tree of honeybees.[38]
Przemysław Prusinkiewicz advanced the idea that real instances can be in part understood as the expression of certain algebraic constraints on free groups, specifically as certain Lindenmayer grammars.[39]
A model for the pattern of florets in the head of a sunflower was proposed by H. Vogel in 1979.[40] This has the form
where n is the index number of the floret and c is a constant scaling factor; the florets thus lie on Fermat's spiral. The divergence angle, approximately 137.51°, is the golden angle, dividing the circle in the golden ratio. Because this ratio is irrational, no floret has a neighbor at exactly the same angle from the center, so the florets pack efficiently. Because the rational approximations to the golden ratio are of the form F(j):F(j + 1), the nearest neighbors of floret number n are those at n ± F(j) for some index j which depends on r, the distance from the center. It is often said that sunflowers and similar arrangements have 55 spirals in one direction and 89 in the other (or some other pair of adjacent Fibonacci numbers), but this is true only of one range of radii, typically the outermost and thus most conspicuous.[41]
Dengan kata lain, ambil contoh td : 55/34 = 1.6176 ; 144/89 =1.61797 ; 1597/987 = 1.618 ~ semakin menghampiri golden ratio = 1.618.
Subhanallah - Sahabat Insaf


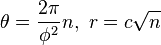


No comments:
Post a Comment